What is semantics syntax?

Another great basics topic, which came up in the comments from last fridays “logic” post, is the
difference between syntax and semantics. This is an important distinction, made in logic, math, and
computer science.

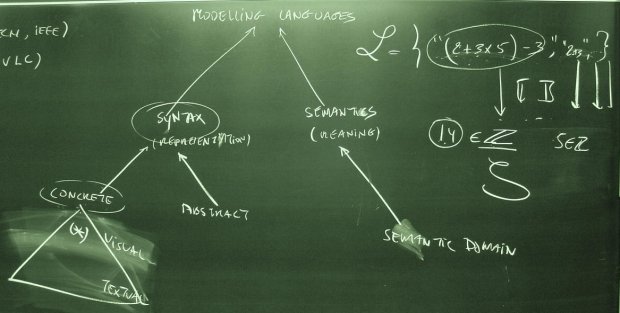
The short version of it is: syntax is what a language looks like; semantics is what
a language means. It’s basically the distinction between numerals (syntax) and
numbers (semantics).

In terms of logic, the syntax is a description of what a valid statement looks like: what the pieces of a statement are, and all of the different ways that the pieces can get put together to
form valid statements. The way that they’re put together also imply how you can take them apart – that is, if you know that a predicate is a predicate name, followed by parens containing arguments to the predicate separated by commas, then given a valid predicate, you can say what the predicate name is, and what the arguments to the predicate in that statement are.

The semantics are the meanings of the statements – and the rules that tell you how to
take a syntactically valid statement, and figure out what it means. So, for example, it includes rules that describe how to find out what object/entity is referred to by a particular primitive name, and what kind of property is meant by a particular predicate.

So, for example, I can show you a simple statement: P("m", "f"). Just by looking at it, you now that it’s a simple predicate statement over two primitives. You can tell that the
name of the predicate is “P”, and that the two arguments to the predicate are “m” and “f”. But what does it mean? That, you can’t find out until I tell you what the semantics of the statement are.

Now, suppose I tell you “P” is a predicate with two parameters, that says the second
parameter is a parent of the first; that “m” is me; and that “f” is my father, then you can see that the meaning of the statement is “My father is one of my parents”.

One of the interesting things about logic inference rules is that they are semantics independent – given a set of statements in FOPL, I don’t need to know what the predicates mean, or what objects are represented by the primitives. I can still perform inferences,
generating new true statements without knowing what they mean. But after I’ve got the
result of the inferences, if you tell me what the predicates mean and what the primitives represent, the statements that I inferred will be true – even though I didn’t know what I was reasoning about when I did the inference.