
Formal semantics programming languages
Starting with basic set theory, structural operational semantics is introduced as a way to define the meaning of programming languages along with associated proof techniques. Denotational and axiomatic semantics are illustrated on a simple language of while-programs, and fall proofs are given of the equivalence of the operational and denotational semantics and soundness and relative completeness of the axiomatic semantics. A proof of Godel's incompleteness theorem, which emphasizes the impossibility of achieving a fully complete axiomatic semantics, is included. It is supported by an appendix providing an introduction to the theory of computability based on while-programs.
Following a presentation of domain theory, the semantics and methods of proof for several functional languages are treated. The simplest language is that of recursion equations with both call-by-value and call-by-name evaluation. This work is extended to lan guages with higher and recursive types, including a treatment of the eager and lazy lambda-calculi. Throughout, the relationship between denotational and operational semantics is stressed, and the proofs of the correspondence between the operation and denotational semantics are provided. The treatment of recursive types - one of the more advanced parts of the book - relies on the use of information systems to represent domains. The book concludes with a chapter on parallel programming languages, accompanied by a discussion of methods for specifying and verifying nondeterministic and parallel programs.

|
Kubuntu 10.04 Desktop Edition Software (Amazon)
|






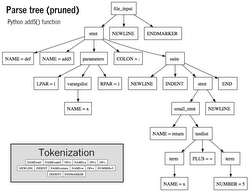 A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely.
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely.